This post will discuss how to approach enthalpy of solution calculations. This is in Module 4 of the current NSW Stage 6 curriculum, and as such is assumed knowledge but not directly examinable in the HSC. So in some sense, agreeing upon one method to use internally in your teaching and assessments (e.g. the one your textbook uses) is a good way to go.

That having been said, we can estimate the heat capacity (=mass × specific heat capacity) of a solution in the following ways (there are also others):

1. Measure it directly (e.g. measure masses and make solution of desired concentration, then transfer a known amount of energy and measure temperature change). This is possible but fairly impractical.

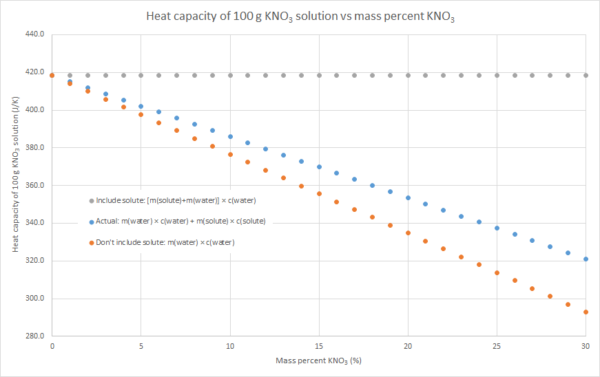
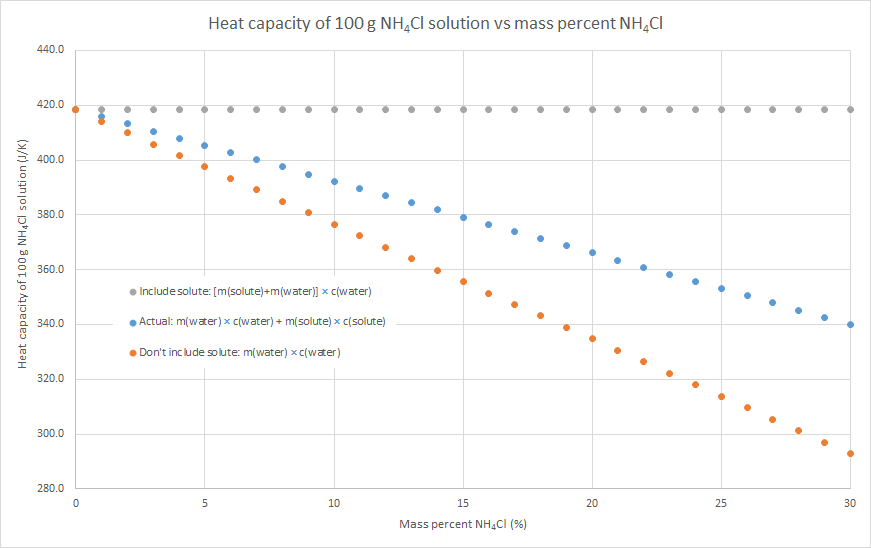
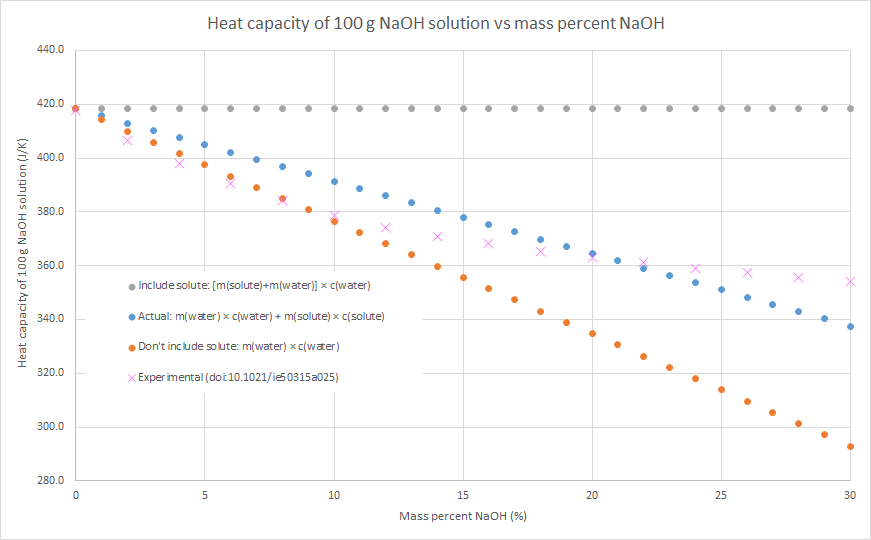
2. If you know the mass and specific heat capacity of both the solute and solvent (e.g. water), then the heat capacity of the solution can be estimated as m(water) × c(water) + m(solute) × c(solute)

Generally we can’t (or aren’t) doing either of those, so we need more approximate methods. For example:

3. We can assume that the salt contributes to the overall heat capacity of the solution identically to water, i.e. the heat capacity of the solution = m(solute) × c(water) + m(water) × c(water). This will overestimate the heat capacity of the solution, as c(solute) < c(water) for most (all?) ionic solutes.

4. We can assume that the salt contributes nothing to the overall heat capacity of the solution. i.e. the heat capacity of the solution = m(water) × c(water). Effectively we are assuming that m(solute) × c(solute) = 0, so this will underestimate the heat capacity of the solution. The following graphs demonstrate this for the three salts that my class used for this practical this year: sodium hydroxide, potassium nitrate and ammonium chloride (the NaOH graph also has some literature data). Blue dots are method 2, grey dots are method 3, orange dots are method 4. As can be seen in the graphs, the value from method 2 is in between the values from methods 3 and 4, but method 4 always gives the better approximation. This is because c(water) is usually much larger than c(solute) for an ionic solute, and m(solute) is usually relatively small compared to the m(water). In such cases, m(water) × c(water) >> m(solute) × c(solute), so the assumption that m(solute) × c(solute) = 0 isn’t a terrible one.